数学の文章を読んでるとコンマ( , )について論理的な意味についてはあまり注意を払うことはないかもしれません。

しかし実際は、文脈によって‘かつ’ もしくは ‘または’の意味で使われており、意味を取り違えると大変なことになります。

そもそも学校教育や教科書でコンマについてはほとんど触れられていないので、多くの人はなんとなしに見過ごしがちです。

一つ例をだしましょう。連立不等式

ｘ²＋４ｘ＋３＞０・・・①
ｘ²ー４ｘー５＜０・・・②
を満たすｘの範囲を求めよ

まずは①と②のそれぞれの範囲を求める。

ｘ²＋４ｘ＋３＞０
（ｘ＋１）（ｘ＋３）＞０
よってｘ＜－３,ー１＜ｘ　・・・③
(ここでのコンマは‘または’の意味に解釈されています！)

ｘ²ー４ｘー５＜０
（ｘ－１）（ｘ＋５）＜０
よってー５＜ｘ＜１　・・・④

わかりやすいように、③と④を数直線上に図示しましょう。

 

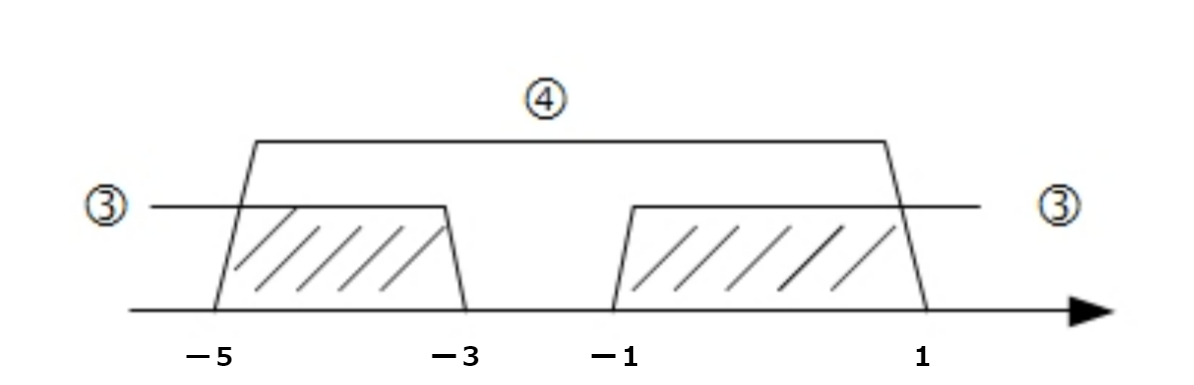
③と④のかぶっている部分がｘ²＋４ｘ＋３＞０,ｘ²ー４ｘー５＜０の範囲なので(ここでのコンマは‘かつ’の意味で解釈されています！)、

－５＜ｘ＜ー３,ー１＜ｘ＜１が答えとなる。(ここでのコンマは‘または’の意味に解釈されています)

どうでしょうか？もし③のコンマがかつの意味で解釈されたらそれを満たすｘの範囲はありませんから、したがって連立不等式を満たすｘの範囲もありません。

他にも集合での記法

A∩B={ｘ| ｘ∈A, x∈B}

と書かれたら、条件文のコンマは‘かつ’の意味で使われるのが慣習のようです。

つまりコンマの論理的な扱いは文脈や慣習によって判断するので、定まったルールがあるわけではありません。

そういわれると明確なルールがなくて困るかもしれないと思われるかもしれませんが、数学に多少なりとも慣れれば困ることはありません。

重要なのはどちらの意味にも使われることがあるということを頭の隅にでもいれておけば十分です。

個人的にはコンマの扱いについては松坂和夫先生の著作の中で触れられていて、感銘を受けたのを覚えています。

まさに喉に刺さった小骨のように心に引っかかってたものがポロリと取れた気分でした。

こういう小さいことって当たり前すぎて文章として残ることがほとんどないので、この記事が私と同じように喉に小骨が刺さっている人に届けば幸いです。